5. Full Well Capacity of the pnCCD¶
5.1. Introduction¶
The amount of charge that can be accumulated in an individual pixel is defined by its full well capacity, and depends primarily on the pixel dimensions. Other design factors can also affect pixel charge capacity, including the requisite operational voltages. Saturation can be theoretically defined on the basis of full well conditions, but the complexity of potential well physics prevents simply considering well capacity as a performance parameter. It is common for CCD imagers to exhibit some effects of approaching a saturation condition before full well capacity is actually reached. As an example, the apparent sensitivity of a CCD may decrease with increasing average signal level because changes in charge transfer dynamics reduce the probability of electron trapping in potential wells nearing saturation. A possible result is increasing deviation by the CCD from linear response, even before blooming artifacts appear. In other words, if pixel saturation is considered to correspond to full well conditions, one early indication of its occurrence is the observation that increasing specimen illumination intensity does not result in additional signal detection; further charge accumulation may subsequently produce visible blooming artifacts. The quantitative capabilities of the CCD are compromised when its response deviates from linearity, and, as previously described, this may occur for some sensor designs before any visual effects of blooming are apparent. Blooming occurs when the charge in a pixel exceeds the saturation level and the charge starts to fill (or overflows) the adjacent pixels.
Certain anomalies in noise characteristics provide another indication of the approach to sensor saturation. Under illumination conditions in which the CCD is operating in the shot noise dominated regime, as light intensity and signal increase, random noise increases as the square-root of the signal. At some illumination level approaching the onset of full well, the positive random noise variations, which add to signal level, begin to be clipped, or smoothed. This phenomenon, termed noise clipping, causes the average noise level to begin to decrease, even while signal is increasing (see panel (a) in Fig. 5.1). At full well conditions, the noise decreases suddenly as charge is spread among neighboring pixels (blooming), while the signal remains stable. When Photon Transfer Curves (PTC) are constructed, plotting noise as a function of average signal, noise increases with signal at a slope governed by the dominant noise regime (see panel (b) in Fig. 5.1). Full well conditions, and the onset of blooming, results in an obvious break in the slope of the curve.
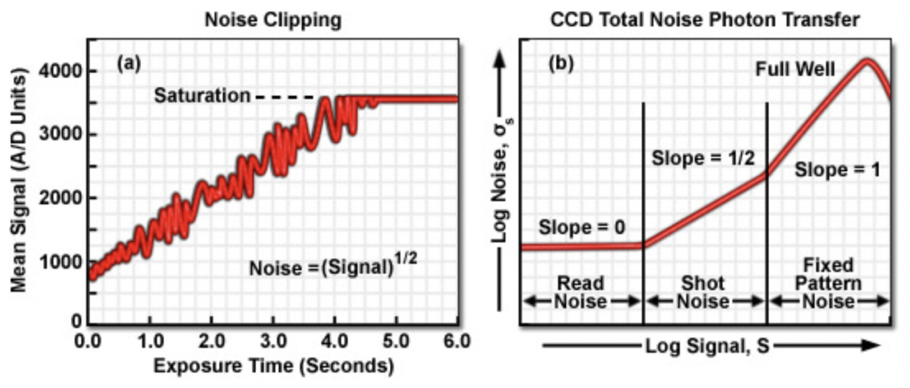
Fig. 5.1 The Photon Transfer Curve (PTC) is a log-log plot of noise versus signal level, from which full well capacity can be determined. The diagram is taken from here.
To understand the plot shown in Fig. 5.1, three types of noise are defined:
- Read noise: This is represented by the first (flat) region of panel (b) of the graph in Fig. 5.1 and is the random noise that is associated with the CCD output amplifier and the camera’s signal-processing electronics. It tells you the minimum observed signal, and it is used to compute dynamic range. Read noise is directly measured from the PTC by recording the noise level at zero illumination.
- Shot noise: Shown in the second region of panel (b) of the graph in Fig. 5.1, it is inherent in the light itself. The noise does not originate in the camera. As the input light level increases in amplitude, the noise at the camera output rises out of the read-noise region and becomes dominated by shot noise. Shot noise is directly related to the input illumination and is proportional to the square root of that signal. The rms value of shot noise is equal to the square root of the mean number of photons incident on a given pixel. Thus, the shot noise profile becomes a straight line with a slope of \(1/2\) on the log-log plot.
- Fixed-pattern noise: The right-most region of the PTC represents the fixed-pattern noise, which becomes dominant at relatively high levels of illumination. This noise results from differences in sensitivity among individual pixels or from photo response nonuniformity. It is directly proportional to input signal strength.
As illumination levels are increased, the individual CCD pixels are unable to hold any additional charge without spilling over into adjacent wells (blooming). At this point on the noise curve, output noise abruptly drops because the signal value is clipped at the pixel’s maximum saturation level. At the point where the PTC peaks, as shown in panel (b) of Fig. 5.1, the CCD is said to have reached full-well capacity.
As described in Fig. 5.1, once the noise at each illumination level is calculated, a PTC is generated by plotting the camera’s output average standard deviation (rms of noise) vs. average signal level on a log-log plot. Then readout noise is directly available from the PTC by recording the noise level at zero illumination (readout noise is the point on the y-axis where background subtracted signal is zero). The full-well capacity parameter is the signal level at the point where the PTC drops. The conversion gain \(G\) of camera systems is typically expressed in \(e^{-}/ADU\). To obtain this gain, on the PTC plot, one should fit the shot noise section by a linear function (\(y\,=\,mx\,+b\)) using regression fitting method. \(G\) can then be found by extrapolation of the regression line towards the crossing with the horizontal axis. In other words, \(G\,=\,10^{-b/m}\) in \(e^{-}/ADU\). Full well capacity is derived from the maximum analog-to-digital output counts and the gain:
where \(S_{max}\) is the maximum analog-to-digital output (in ADU) before the PTC begins to slope downward, and \(FWC\) is the full well capacity in number of electrons. Finally, the dynamic range, which evaluates the ability of the camera to record low intensity signals alongside high intensity signals becomes:
where \(DR\) is the dynamic range expressed in dB, and \(\sigma\) is the read noise. Here, \(FWC\) and \(\sigma\) are both in units of number of electrons. Therefore, the limiting factors for the dynamic range are the full well capacity, which defines the maximum signal of the detector and the read noise of the detector which determines the lowest meaningful signal.
5.2. Obtaining Full Well Capacity of the pnCCD¶
In order to obtain the pnCCD full well capacity, we took some high intensity data during the commissioning of the new pnCCD detector in August - 2020. The runs are summarized in Table 5.1 to Table 5.4.
pnCCD Gain |
Photon Energy (keV) |
Pulse Energy (mJ) |
Temperature Top/Bottom (degC) |
Run | Dark Run |
Voltage Top/Bottom |
| 1/340 | 1.8 | 1.842 | -35 / -33 | 129 | 132 | -440/-450 |
| 1/340 | 1.8 | 1.842 | -35 / -33 | 130 | 132 | -440/-450 |
pnCCD Gain |
Photon Energy (keV) |
Pulse Energy (mJ) |
Temperature Top/Bottom (degC) |
Run | Dark Run |
Gas/ Solid |
Bunches |
| 1/256 | 1.8 | 1.94 | -35 / -29 | 164 | 170 | 1.4/11.4 | 50 |
| 1/256 | 1.8 | 1.94 | -35 / -29 | 166 | 170 | 2.9/11.4 | 50 |
| 1/256 | 1.8 | 2 | -35 / -30 | 167 | 170 | 1.4/11.4 | 25 |
| 1/256 | 1.8 | 2 | -35 / -30 | 168 | 170 | 1.4/11.4 | 15 |
| 1/256 | 1.8 | 2 | -35 / -30 | 169 | 170 | 1.4/11.4 | 10 |
pnCCD Gain |
Photon Energy (keV) |
Pulse Energy (mJ) |
Temperature Top/Bottom (degC) |
Run | Dark Run |
Proposal |
| 1/64 | 1.8 | 1.9 | -30 / -30 | 86 | 89 | 2720 |
pnCCD Gain |
Photon Energy (keV) |
Pulse Energy (mJ) |
Temperature Top/Bottom (degC) |
Run | Atten | Trans | Filters (microns) |
| 1/16 | 1.8 | 1.98 | -30 / -30 | 76 | 0.006 | 50 | 20 and 10 |
| 1/16 | 1.8 | 1.9 | -30 / -30 | 77 | 1e-5 | 1 | 20 and 10 |
| 1/16 | 1.8 | 1.9 | -30 / -30 | 79 | 11 | 0.47 | 5 and 10 |
The runs mentioned in Table 5.1 are not analyzed becasue full well capacity depends on the bias voltages applied to the detector, and the operating voltages of the top and bottom pnCCD sensors during these runs are not used anymore. Run 86 with gain 1/64 is also not analyzed because it is only one run at one intensity. We are looking at multiple runs with multiple intensities to derive the full well capacity. The three runs with pnCCD gain of 1/16 are analyzed. However, the FEL beam intensity for these runs was too low such that none of the pixels seem to have reached the full well capacity during these runs. Therefore, the analysis is not shown here.
Analyzing the Runs with Gain 1/256:
The data of runs 164, 166, 167, 168 and 169 were background subtracted (based on the dark run 170) and common mode corrected. Fig. 5.2 shows the corrected data for run 166 obtained by shining the highest intensity FEL beam onto a membrane. A lot of pixels in this image show possibility of saturation. The maximum intensity (in ADU) in this image belongs to the pixel with coordinates (row, column) \(=\) (476, 508). Fig. 5.3 shows the background subtracted signal (in ADU) in every image frame from run 166.
We then looked at a few individual pixels and plotted the PTC for these pixels. To obtain these plots, we have calculated the background subtracted and common mode corrected signal per pixel averaged over every 100 image frames. This is done for individual runs 164, 166, 167, 168 and 169. A final array is constructed by concatenating all individual mean signal arrays. The individual arrays are concatenated based on increasing level of FEL intensity. Similarly, the noise is also calculated as the standard deviation per pixel over every 100 image frames for individual runs 164, 166, 167, 168 and 169. A final array is constructed by concatenating all individual mean noise arrays corresponding to the run with the lowest FEL beam intensity to the one with the highest intensity. From the final arrays of mean signal and mean noise, we have constructed the PTCs, which are shown for a few selected pixels in Fig. 5.4 to Fig. 5.7.
To obtain the full well capacity and conversion gain, we have divided the data shown on Fig. 5.4 to 3 sections and have fit each section with a line using linear regression fitting method. The fits are shown in Fig. 5.5. The first fit has a slope of 0.7 and the second fit has the slope of 1.4. Therefore, these two sections represent the shot noise and fixed pattern noise (see Fig. 5.1), respectively. We do not seem to have FEL beam intensity low enough for this pixel to be able to observe the read noise section. The conversion gain is calculated from the shot noise section. An intersection between the linear fit on the shot noise section of the PTC and the x-axis gives \(\log(G)\), where \(G\) is the conversion gain in \(e^{-}/ADU\). Therefore, we obtain 1.32 \(e^{-}/ADU\) for the conversion gain using the PTC of the pixel with coordinates of (row,column) \(=\) (476,508).
The full well capacity is where the third fit crosses the x-axis, which is 4.498 on a logarithmic scale. Therefore, the full well capacity is \(10^{4.498}\), which is 31461 ADU. We can then use the conversion factor we obtained in \(e^{-}/ADU\) and convert the full well capacity from ADU to number of electrons. Doing so, we arrive at a full well capacity of 41529 \(e^{-}\).
Warning
- The measurement from which full well capacity can be determined must satisfy the conditions of a flat field measurement. In other words, the detector shall be shined on with a flat field FEL beam whose intensity is slowly increased until the saturation is reached. This was not the case for our measurement as can be seen in Fig. 5.2. We had a FEL beam very localized around the center of the CCD and everywhere else was rather dark. Therefore, not all pixels have reached full well capacity, and for this reason, we cannot calculate the full well capacity accross the detector consistently.
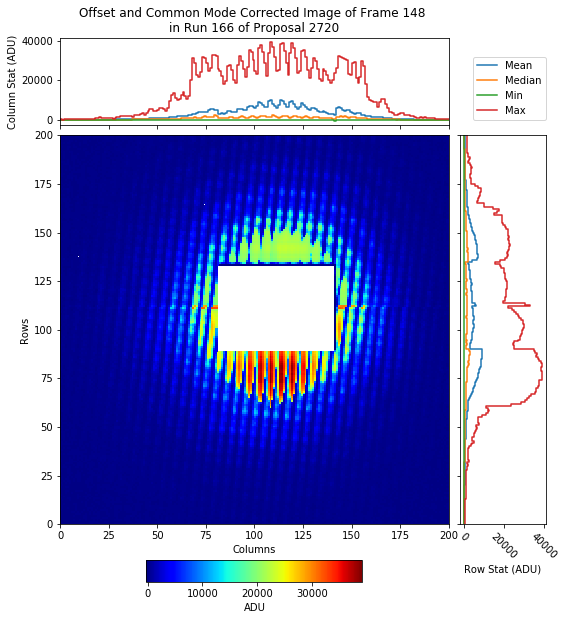
Fig. 5.2 The offset and common mode corrected data from run 166. The image shows the highest intensity (in ADU) recorded in image frame 148. Gain was set to 1/256 and the pnCCD was operating in normal mode.
Fig. 5.3 The offset and common mode corrected signal (in ADU) for every image frame from run 166 in a pixel located in row 476 and column 508. This pixel shows the highest intensity (in ADU) recorded during this run in image frame 148. Gain was set to 1/256 and the pnCCD was operating in normal mode.
Fig. 5.4 The offset and common mode corrected signal averaged over every 100 image frames is calculated at the pixel with coordinates of (row,column) \(=\) (476,508) for individual runs 164, 166, 167, 168 and 169. The individual arrays are concatenated based on increasing level of FEL intensity. The natural logarithm of this final array is shown on the x-axis. The y-axis shows natural logarithm of the mean noise, where the latter is also calculated the same way as mean signal. The gain was set to 1/256 and pnCCD was operating in normal mode. A comparison of this figure and Fig. 5.1, shows that this particular pixel reaches full well capacity after which the pixel is saturated.
Fig. 5.5 The fits of different sections on the PTC plot for a pixel with coordinates of (row,column) \(=\) (476,508). pnCCD gain was set to 1/256 and it was operating in normal mode. The shot noise and fixed pattern noise (see Fig. 5.1) are shown by the first and second fits, respectively. The first and third fits are used to obtain conversion gain(in \(e^{-}/ADU\)) and full well capacity (in ADU), respectively. These values are calculated to be 1.32 \(e^{-}/ADU\) and 31461 ADU, respectively. Using the conversion gain in \(e^{-}/ADU\), we converted the full well capacity in ADU to that in units of electrons and the result is: full well capacity \(=\) 41529 \(e^{-}\).
Fig. 5.6 The PTC plot for a pixel with coordinates of (row,column) \(=\) (548,525). pnCCD gain was set to 1/256 and it was operating in normal mode. This pixel is not saturated because of its location with respect to the area where the FEL beam was shining on the detector. The PTC plot shows the shot noise and part of fixed pattern noise sections. Because this pixel is not saturated, we do not see the full well turning point on this plot. If this plot is fitted by two lines using the linear regression method, the slopes of the lines are 0.531 and 1.7. The former is rather close to the expected slope of 1/2, while the latter is bigger than the expected slope of one for the fixed pattern noise.
Fig. 5.7 The PTC plot for a pixel with coordinates of (row,column) \(=\) (425,425). pnCCD gain was set to 1/256 and it was operating in normal mode. This pixel is far from being saturated because of its location with respect to the area where the FEL beam was shining on the detector. The PTC plot only shows the shot noise section because this pixel is far from saturation. If this plot is fitted by a line using the linear regression method, the slope of the line is 0.466, which is rather close to the expected slope of 1/2 for the shot noise section.