This notebook gives the basic steps in order to perform an azimuthal integration, including pixel splitting, of a scattering pattern recorded with the DSSC detector which has hexagonal spahed pixels.

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.constrained_layout.use'] = True

DSSC geometry

From the quadrants position and the position of the modules inside each quadrants we compute a DSSC geometry

from extra_data import open_run
from extra_data.components import DSSC1M
from extra_geom import DSSC_1MGeometry

quad_pos = [(-122.21101449000001, 2.17217391),
    (-124.4, -118.94881159),
    (1.32336232, -120.39306931),
    (3.1934492800000003, 0.80901765)]
geom_file = "/gpfs/exfel/exp/SCS/201901/p002212/usr/Shared/Training_UP-2719/geometry/dssc_geom_AS_aug20.h5"
geom = DSSC_1MGeometry.from_h5_file_and_quad_positions(geom_file, quad_pos)

We then give this information to pyFAI by creating a detector object from the individuals 6 corner position of each one million pixels.

from pyFAI.azimuthalIntegrator import AzimuthalIntegrator

ai = AzimuthalIntegrator(detector=geom.to_pyfai_detector())

WARNING:silx.opencl.common:Unable to import pyOpenCl. Please install it from: https://pypi.org/project/pyopencl

Load the test data

We then load some test data to test the azimuthal integration.

import xarray as xr
path = '/gpfs/exfel/exp/SCS/202022/p002711/usr/processed_runs/r97'
data = xr.open_mfdataset(path + '/*.h5', parallel=True, join='inner')

data

<xarray.Dataset>
Dimensions:            (pp: 1, bin_nrj: 1, module: 16, y: 128, x: 512,
                        sa1_pId: 200, pulse_slot: 2700)
Coordinates:
  * bin_nrj            (bin_nrj) float64 780.0
  * module             (module) int64 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
  * pp                 (pp) object 'unpumped'
  * sa1_pId            (sa1_pId) int64 600 604 608 612 ... 1384 1388 1392 1396
Dimensions without coordinates: y, x, pulse_slot
Data variables:
    DSSC               (pp, bin_nrj, module, y, x) float64 dask.array<chunksize=(1, 1, 1, 128, 512), meta=np.ndarray>
    SCS_SA1            (module, bin_nrj, sa1_pId) float64 dask.array<chunksize=(1, 1, 200), meta=np.ndarray>
    SCS_SA3            (module, pp, bin_nrj) float64 dask.array<chunksize=(1, 1, 1), meta=np.ndarray>
    bunchPatternTable  (module, bin_nrj, pulse_slot) float64 dask.array<chunksize=(1, 1, 2700), meta=np.ndarray>
    nrj                (module, bin_nrj) float64 dask.array<chunksize=(1, 1), meta=np.ndarray>

xarray.Dataset

• Dimensions:
  • pp: 1
  • bin_nrj: 1
  • module: 16
  • y: 128
  • x: 512
  • sa1_pId: 200
  • pulse_slot: 2700
• Coordinates: (4)
  • bin_nrj
    (bin_nrj)
    float64
    780.0

    array([780.])

  • module
    (module)
    int64
    0 1 2 3 4 5 6 ... 10 11 12 13 14 15

    array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15])

  • pp
    (pp)
    object
    'unpumped'

    array(['unpumped'], dtype=object)

  • sa1_pId
    (sa1_pId)
    int64
    600 604 608 612 ... 1388 1392 1396

    array([ 600,  604,  608,  612,  616,  620,  624,  628,  632,  636,  640,  644,
            648,  652,  656,  660,  664,  668,  672,  676,  680,  684,  688,  692,
            696,  700,  704,  708,  712,  716,  720,  724,  728,  732,  736,  740,
            744,  748,  752,  756,  760,  764,  768,  772,  776,  780,  784,  788,
            792,  796,  800,  804,  808,  812,  816,  820,  824,  828,  832,  836,
            840,  844,  848,  852,  856,  860,  864,  868,  872,  876,  880,  884,
            888,  892,  896,  900,  904,  908,  912,  916,  920,  924,  928,  932,
            936,  940,  944,  948,  952,  956,  960,  964,  968,  972,  976,  980,
            984,  988,  992,  996, 1000, 1004, 1008, 1012, 1016, 1020, 1024, 1028,
           1032, 1036, 1040, 1044, 1048, 1052, 1056, 1060, 1064, 1068, 1072, 1076,
           1080, 1084, 1088, 1092, 1096, 1100, 1104, 1108, 1112, 1116, 1120, 1124,
           1128, 1132, 1136, 1140, 1144, 1148, 1152, 1156, 1160, 1164, 1168, 1172,
           1176, 1180, 1184, 1188, 1192, 1196, 1200, 1204, 1208, 1212, 1216, 1220,
           1224, 1228, 1232, 1236, 1240, 1244, 1248, 1252, 1256, 1260, 1264, 1268,
           1272, 1276, 1280, 1284, 1288, 1292, 1296, 1300, 1304, 1308, 1312, 1316,
           1320, 1324, 1328, 1332, 1336, 1340, 1344, 1348, 1352, 1356, 1360, 1364,
           1368, 1372, 1376, 1380, 1384, 1388, 1392, 1396])

• Data variables: (5)
  • DSSC
    (pp, bin_nrj, module, y, x)
    float64
    dask.array<chunksize=(1, 1, 1, 128, 512), meta=np.ndarray>

    Array Chunk Bytes 8.00 MiB 512.00 kiB Shape (1, 1, 16, 128, 512) (1, 1, 1, 128, 512) Dask graph 16 chunks in 33 graph layers Data type float64 numpy.ndarray

  • SCS_SA1
    (module, bin_nrj, sa1_pId)
    float64
    dask.array<chunksize=(1, 1, 200), meta=np.ndarray>

    Array Chunk Bytes 25.00 kiB 1.56 kiB Shape (16, 1, 200) (1, 1, 200) Dask graph 16 chunks in 49 graph layers Data type float64 numpy.ndarray

  • SCS_SA3
    (module, pp, bin_nrj)
    float64
    dask.array<chunksize=(1, 1, 1), meta=np.ndarray>

    Array Chunk Bytes 128 B 8 B Shape (16, 1, 1) (1, 1, 1) Dask graph 16 chunks in 49 graph layers Data type float64 numpy.ndarray

  • bunchPatternTable
    (module, bin_nrj, pulse_slot)
    float64
    dask.array<chunksize=(1, 1, 2700), meta=np.ndarray>

    Array Chunk Bytes 337.50 kiB 21.09 kiB Shape (16, 1, 2700) (1, 1, 2700) Dask graph 16 chunks in 49 graph layers Data type float64 numpy.ndarray

  • nrj
    (module, bin_nrj)
    float64
    dask.array<chunksize=(1, 1), meta=np.ndarray>

    Array Chunk Bytes 128 B 8 B Shape (16, 1) (1, 1) Dask graph 16 chunks in 49 graph layers Data type float64 numpy.ndarray

• Indexes: (4)
  • bin_nrj
    PandasIndex

    PandasIndex(Float64Index([780.0], dtype='float64', name='bin_nrj'))

  • module
    PandasIndex

    PandasIndex(Int64Index([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15], dtype='int64', name='module'))

  • pp
    PandasIndex

    PandasIndex(Index(['unpumped'], dtype='object', name='pp'))

  • sa1_pId
    PandasIndex

    PandasIndex(Int64Index([ 600,  604,  608,  612,  616,  620,  624,  628,  632,  636,
                ...
                1360, 1364, 1368, 1372, 1376, 1380, 1384, 1388, 1392, 1396],
               dtype='int64', name='sa1_pId', length=200))

• Attributes: (0)

img = data['DSSC'].squeeze()
img.shape

(16, 128, 512)

from matplotlib.colors import LogNorm
from matplotlib.patches import Circle

geom2 = geom.offset((0, 0))

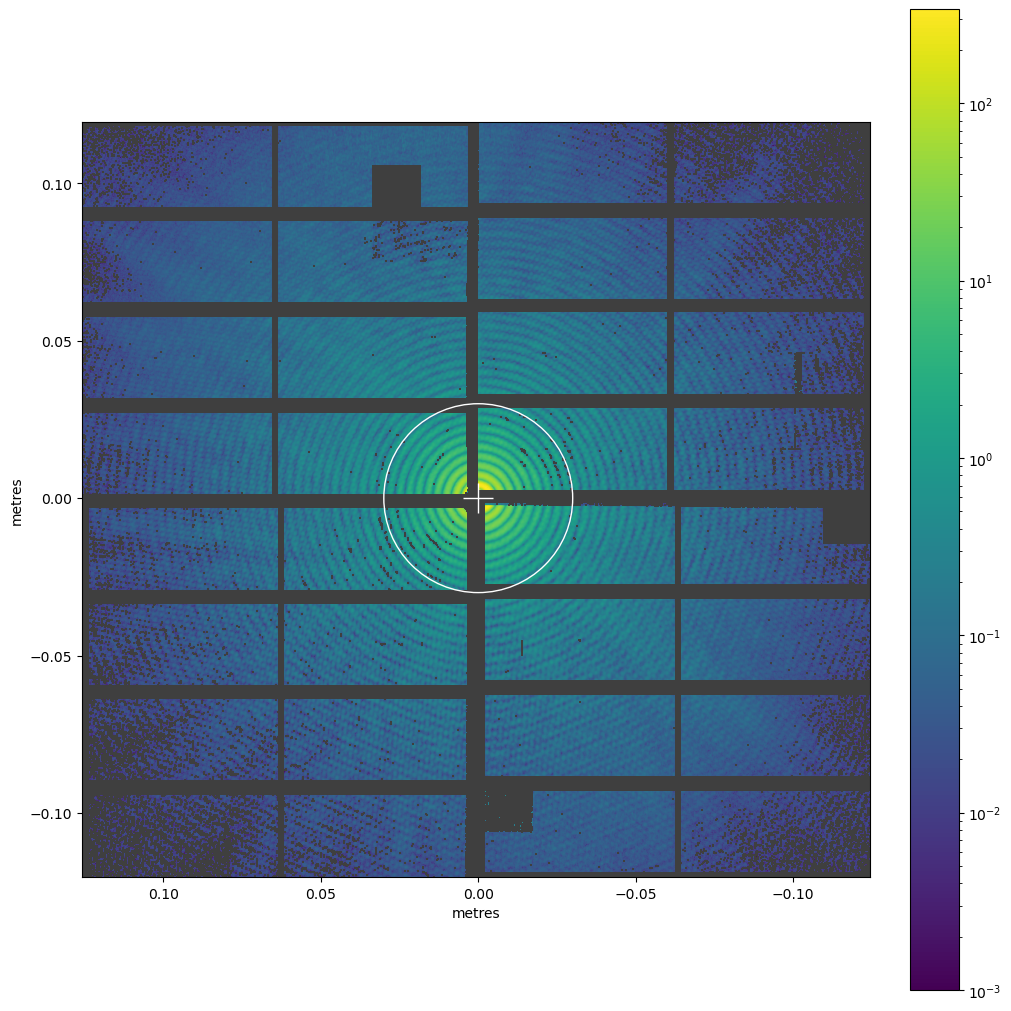
ax = geom2.plot_data_fast(img, colorbar=True, norm=LogNorm(), vmin=1e-3, axis_units='m')
ax.add_patch(Circle((0, 0), radius=0.03, fill=False, color='white'))

<matplotlib.patches.Circle at 0x2ba9de743190>

joined = img.values.reshape(16*128, 512)

cake_bbox, q, chi = ai.integrate2d(
    joined,
    npt_rad=900,
    unit='r_mm',
    correctSolidAngle=False,
    method="bbox",
)

cake_nosplitting, q, chi = ai.integrate2d(
    joined,
    npt_rad=900,
    unit='r_mm',
    correctSolidAngle=False,
    method="no",
)


fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(15, 10))

im0 = ax0.imshow(cake_nosplitting, aspect='auto', norm=LogNorm(), vmin=1e-3)
ax0.set_title('No splitting')
cbar = fig.colorbar(im0, ax=ax0)

im1 = ax1.imshow(cake_bbox, aspect='auto', norm=LogNorm(), vmin=1e-3)
ax1.set_title('bbox splitting')
cbar = fig.colorbar(im1, ax=ax1)

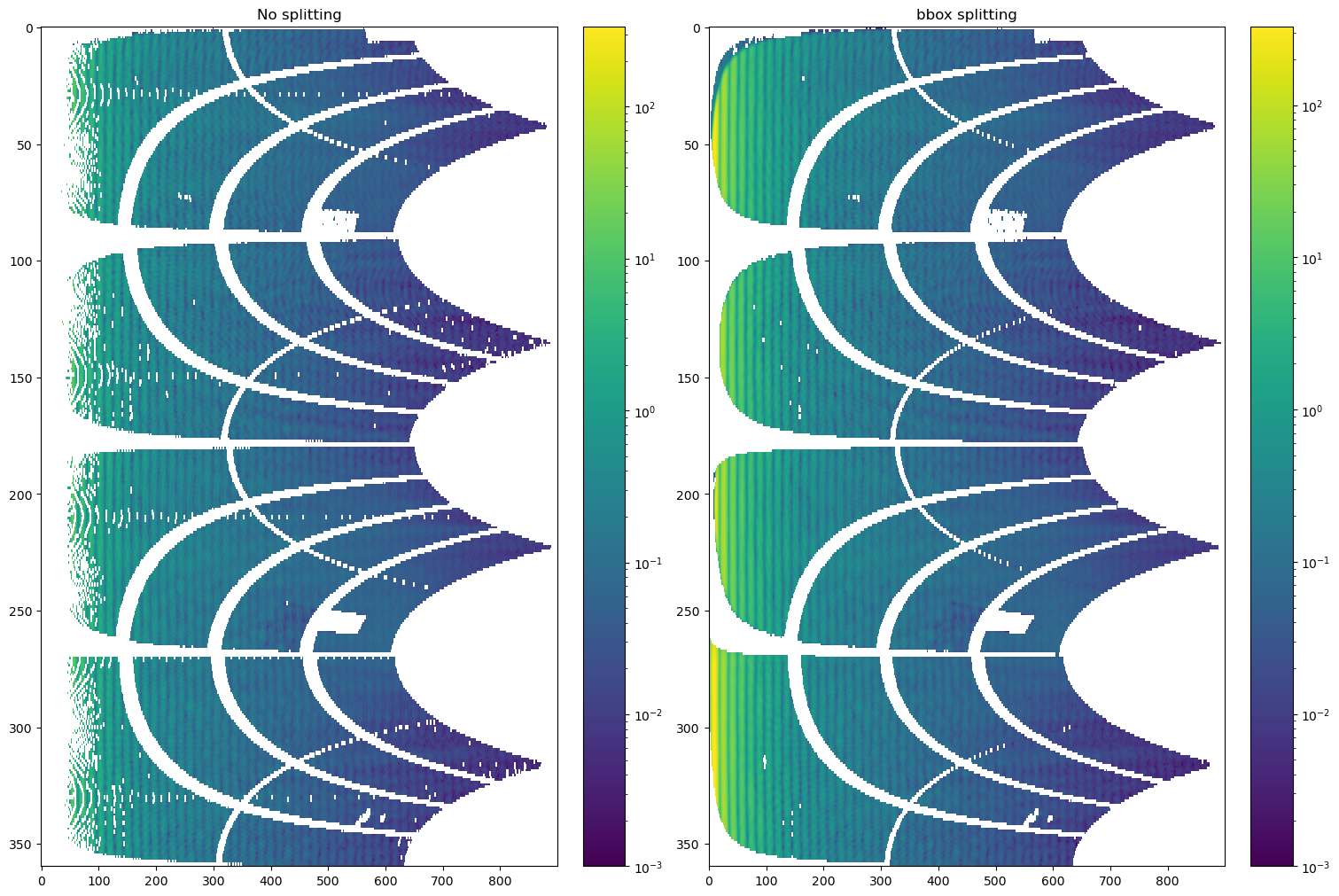
We can confirm that pixel splitting improves the data representation in the low-q range.

rint_no, I_no = ai.integrate1d(
    joined,
    npt=900,
    unit='r_mm',
    method='no'
)

rint_bbox, I_bbox = ai.integrate1d(
    joined,
    npt=900,
    unit='r_mm',
    method='bbox'
)

plt.figure()
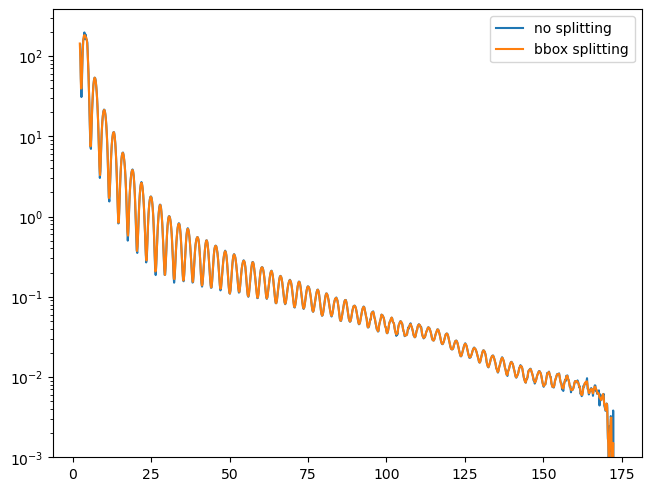
plt.semilogy(rint_no, I_no, label='no splitting')
plt.semilogy(rint_bbox, I_bbox, label='bbox splitting')
plt.ylim(bottom=1e-3)
plt.legend()

<matplotlib.legend.Legend at 0x2babe9cdf4c0>