HRIXS: The Heisenberg Resonant Inelastic X-Ray Scattering Spectrometer¶
Technical movement¶
The movements of the HRIXS are controlled by a PLC. On the PLC level we assure that the spectrometer cannot be moved outside of its safe working conditions, as defined by the instruction manual.
Two of those parameters are trivial, the grating postion G (motor GTZ)
and the detector position D (motor DTZ) simply have a minimum and a
maximum value.
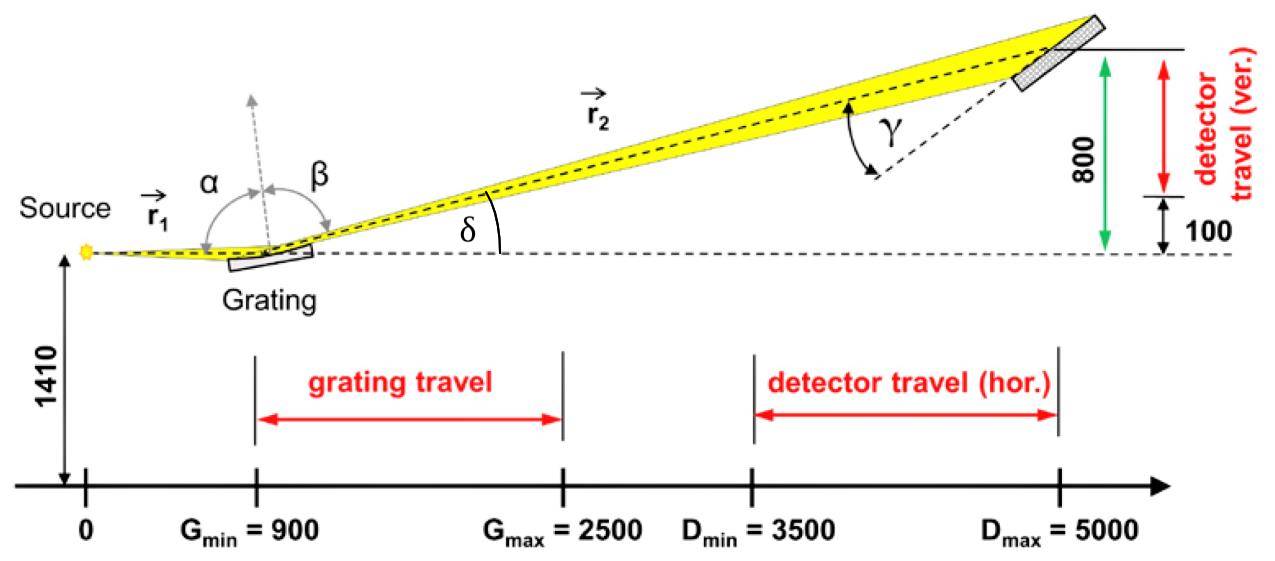
Geometry of the HRIXS, from Figure 35 (page 79) in the instruction manual
The height Y of the detector should be kept such that the angle δ of the
detector is below 15°. So the detector height should be calculated from
Y = (D - G) tan δ. The height is adjusted using the two motors DTY1
and DTY2, which always must move in parallel.
It is also important that the detector pitch follows this angle δ, but it
needs to be adjustable by a small angle ɣ, -5° < ɣ < 5° (ɣ is shown
exaggerated in the figure). So the detector pitch θ (motor DRX)
is θ = δ + ɣ.
Summarizing, we have four parameters, D, G, δ and ɣ, from which the motor positions are calculated as follows:
GTZ= GDTZ= DDTY1=DTY2= (D - G) tan δDRX= δ + Ɣ
Solution using interlocks¶
Unfortunately, it is not as easy as desired to implement coupled motions as described above on the PLC level, so also this will be done in Karabo. Instead, the PLC will only have interlocks which stop all four motors mentioned above if we leave the safe range of parameters.
Solving the above equations leads to the following inequalities:
DRX> arctan(DTY/ (DTZ-GTZ)) - 5°DRX< arctan(DTY/ (DTZ-GTZ)) + 5°DTY< (DTZ-GTZ) tan 15°
These must be fulfilled at all times, otherwise all mentioned motors must stop. In order to get out of an interlocked condition one can move the motors on the left side of the inequalities such that those are again fulfilled.
At the same time, the distance between grating chamber (GTZ) and detector chamber (DTZ) should remain between 2190 mm and 3242 mm. So
DTZ-GTZ< 3242 mmDTZ-GTZ> 2190 mm
Physical parameters¶
The HRIXS uses a variable line spacing (VLS) grating to disperse the incoming X-Ray beam onto a detector. Two different gratings are available, with a nominal line spacing of n0 = 1000 lines / mm or n0 = 3000 lines / mm. Calculations of such a grating can be found in Svitozar Serkez’ Thesis on page 37.
We need to calculate the parameters for the technical movement as described above from the photon enery E and the diffraction order m.
The grating equation applies, with entrance angle α and exit angle β we have
where m is the diffraction order and λ is the wavelength. (Obviously E λ = hc with Planck’s constant h and the speed of light c)
The VLS grating focusses the beam onto the detector following
where n1 represents the linear chirp of the grating spacing, R is the radius of curvature of the grating, and r1 and r2 are the lenght of the entrance and exit arm of the spectrometer.
The coma abberation is minimized if
where n2 represents the linear and quadratic chirp of the grating spacing.
By now we have four physical parameters (α, β, r1, r2) but only three equations. As a fourth equation we could use the position of the sagittal focus, as proposed by Svitozar. But usually this is not a critical parameter, so instead we leave one variable free (r1), and use this variable to optimize resolution vs. transmission: if the grating is close to the source, we improve transmission, if it is further away, we improve the resolution.
The technical parameters can be calculated as follows: D = r1, α + β + δ = 180°, and G - D = r2 cos δ.